Самая красивая и фундаментальная математическая картина: скатер
Предыстория
1963 год. На очередном семинаре польский математик Станислав Улам откровенно скучает. Вместо того, чтобы слушать докладчика, он чертит на бумаге сетку для шахматного этюда, но вместо этого начинает нумеровать клетки своей тетради по спирали:

Чисто интуитивно Станислав начинает отмечать простые числа, т.е. те, которые нацело не делятся ни на какие числа, кроме себя и единицы:

Уже даже на таком небольшом рисунке ему становится ясно, что простые числа удивительным образом выстраиваются по диагоналям или, как сказал Улам, " проявляли сильно неслучайное поведение". Добравшись до институтской ЭВМ, математик вместе с коллегами построил этот паттерн для 90 миллионов чисел и получил т.н. скатерть Улама или спираль простых чисел:

В чем математическое значение скатерти Улама ?
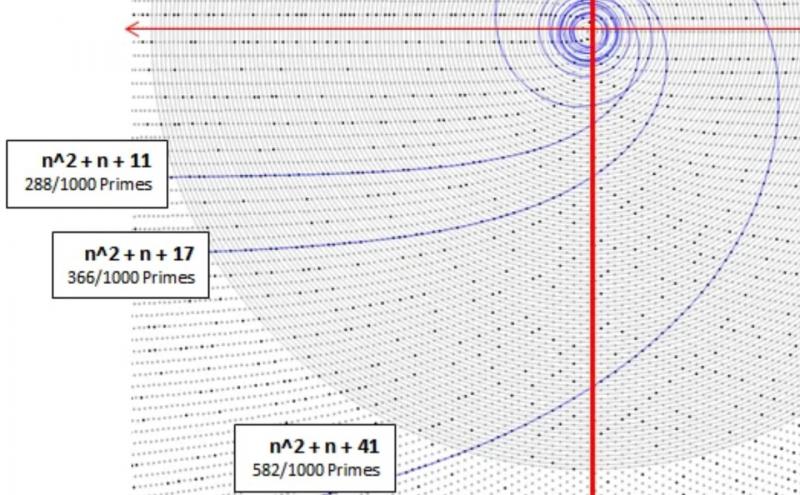
Диагонали, на которых лежат простые числа описываются квадратным трехчленом вида: ax^2+bx+c, что позволяет быстро выделять такие многочлены, порождающие простые числа, что является важной криптографической задачей. Например, вот известный порождающий трехчлен Эйлера: x^2+x+41, значение которого для любого числа меньше 40 является простым числом:
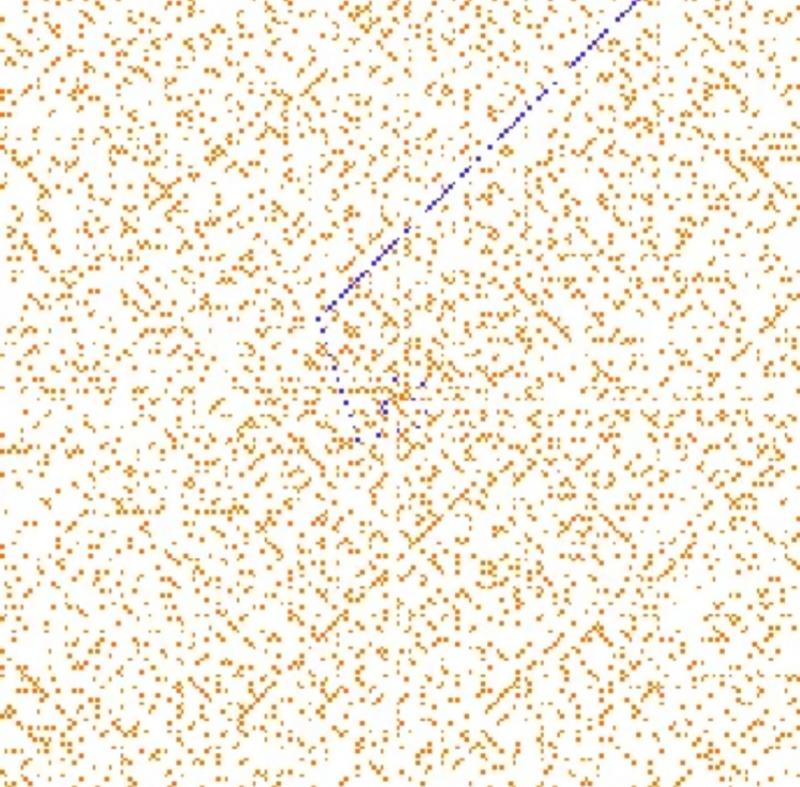
Пройдя по пути Улама, математики начали предлагать другие, иногда даже более удобные, визуализации. Например, спираль Сакса, построенная по следующему принципу в полярной системе координат. Для каждого числа его расположение на спирали Сакса определяется расстоянием r и углом θ . Например, для числа 16, радиус - это √ 16 = 4, а угол θ =2π*4=8π, т.е. это число расположено строго на восток. Если взять больше чисел, получится завораживающая картина:

В спирали Сакса простые числа располагаются на кривых линиях, называемых "кривыми произведений". Так как они закручиваются в бесконечность, с их помощью можно предсказывать появление гигантских простых чисел, что очень нравится криптографам, т.к. чем больше простое число, тем труднее "взломать" шифр, на основе которого он создан (очень грубое описание).
1963 год. На очередном семинаре польский математик Станислав Улам откровенно скучает. Вместо того, чтобы слушать докладчика, он чертит на бумаге сетку для шахматного этюда, но вместо этого начинает нумеровать клетки своей тетради по спирали:

Чисто интуитивно Станислав начинает отмечать простые числа, т.е. те, которые нацело не делятся ни на какие числа, кроме себя и единицы:

Уже даже на таком небольшом рисунке ему становится ясно, что простые числа удивительным образом выстраиваются по диагоналям или, как сказал Улам, " проявляли сильно неслучайное поведение". Добравшись до институтской ЭВМ, математик вместе с коллегами построил этот паттерн для 90 миллионов чисел и получил т.н. скатерть Улама или спираль простых чисел:

В чем математическое значение скатерти Улама ?
Диагонали, на которых лежат простые числа описываются квадратным трехчленом вида: ax^2+bx+c, что позволяет быстро выделять такие многочлены, порождающие простые числа, что является важной криптографической задачей. Например, вот известный порождающий трехчлен Эйлера: x^2+x+41, значение которого для любого числа меньше 40 является простым числом:

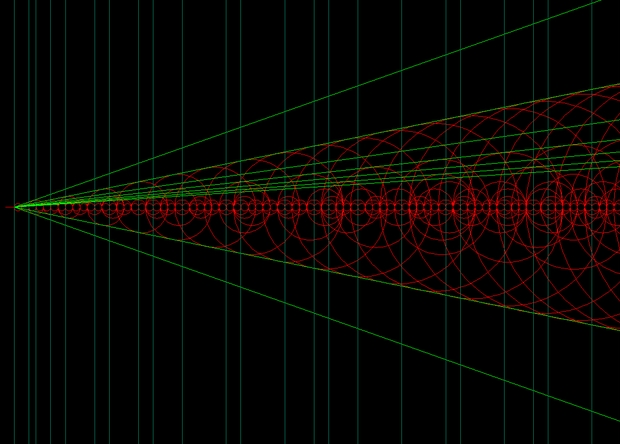
Пройдя по пути Улама, математики начали предлагать другие, иногда даже более удобные, визуализации. Например, спираль Сакса, построенная по следующему принципу в полярной системе координат. Для каждого числа его расположение на спирали Сакса определяется расстоянием r и углом θ . Например, для числа 16, радиус - это √ 16 = 4, а угол θ =2π*4=8π, т.е. это число расположено строго на восток. Если взять больше чисел, получится завораживающая картина:

В спирали Сакса простые числа располагаются на кривых линиях, называемых "кривыми произведений". Так как они закручиваются в бесконечность, с их помощью можно предсказывать появление гигантских простых чисел, что очень нравится криптографам, т.к. чем больше простое число, тем труднее "взломать" шифр, на основе которого он создан (очень грубое описание).




Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.